どんな人に読んで欲しい?周波数分析したい人
どーも!エンジニア + データサイエンティスト / 2 =虎ぱぱです(*’ω’*)
機械メーカのエンジニアとして計測データの分析を主な生業としてます。
FFT解析を初めてやった時はもう訳がわからず地獄のような苦しみを味わいました。笑
始めてFFT解析を行う方が、飽きずに概要を掴めるように『式をなるべく使わずに』解説したいと思います。
私のキャリア、人となりが書いてありますので、こちらも併せて読んでみて下さい!!

この記事を読むとFFT解析の概要がつかめます。こんな方におすすめ!!☟
- 音や振動を分析する技術者の卵。PAさんなど
- 機械学習やAIエンジニアでFFT解析を特徴量として扱う人
- 分光学・電気工学系の研究者,学生さん
- スペクトル解析っ調べたら難しい式ばかりで嫌になった人
FFT解析は現在様々なツールで実施できます。プログラミングで実施する場合も、関数を使えば簡単にできてしまいます。
なので、難しい演算を全て理解する必要はないと思います。
ただし、解析ツールを使用する上で、最低限抑えておかなきゃいけないポイントはあります。
この記事では極力、式を使わずFFTについてわかりやく説明していきます。
FFT解析って何?3ステップで解説
ステップ1 FFT=高速フーリエ変換
FFTは『Fast Fourier Transform』の略語です。日本語にすると『高速フーリエ変換』です。
そのままの意味で、フーリエ変換を早く行うための手法です。
高速に『離散フーリエ変換』を行うアルゴリズムのことです。
ステップ2 フーリエ変換は周波数分析の手法
フーリエ変換は周波数分析=スペクトル分析の手法の一つです。
周波数分析の概要について説明しますが、そもそも周波数って何?という人はこちらを先に読んでもらいたいです!!

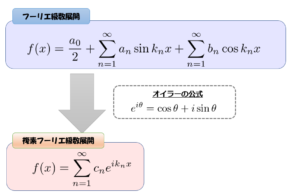
一応式に触れておきますが、フーリエ変換の元になっているのはフーリエ級数展開という手法です。
出展元:宇宙に入ったカマキリ さん
フーリエ級数展開はとても複雑な計算が必要で、複素数・三角関数を十分に理解してからでないと恐らく解けません。まずはできることが大切。理屈は後から学びましょう。とりあえず今は、ふ~ん。くらいに思っといてください。
下手に専門用語を並べて説明すると余計わからなくなると思いますので、データを使って説明します。
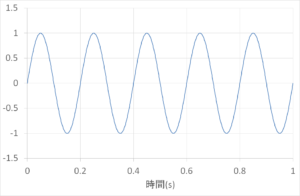
横軸が時間なので…1秒間に5回の山!!これは5Hzのsin波です。当ブログ上では何回も登場してます。
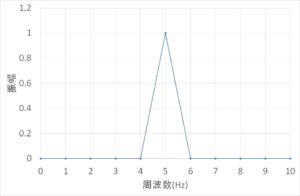
この波形をフーリエ変換するとこうなります。
横軸は周波数、縦軸は振幅です。縦軸は解析前と基本的に変わりません。(縦軸の値は解析条件により異なるので注意。この場合はリニア)
さっきの横軸が時間のグラフで周波数がいくつ?というのを調べようとすると、1秒間あたりの波の数を数えるしかありませんでしたが、フーリエ変換を行うことで、データの周波数と振幅が一目瞭然になりました。
ステップ3 周波数分析の活用『音』を例に説明
様々なジャンルの勉強に対して言えますが、何のために使うかを理解しないと、内容を理解し辛いですよね?
ここでは周波数分析≒フーリエ変換は世間でどのようなことに活用されているかを説明します。
IoTや故障診断全盛期の今、工学系のデータ分析で、音や振動の分析は外せないのではないでしょうか。
この世に音や振動ってたくさん存在しますよね?実は音と振動はほとんど同じです。伝達方法が違うだけです。
音が空気中を伝わるのに対し、振動は物体を通じて伝わる。そんなイメージです。
楽器の音も全て周波数をコントロールすることで成り立っています。周波数が低い=音が低いということです。
この動画をご覧いただくと、わかりやすいと思います。周波数によって音が変わります。(再生の際は音量に注意してください!)
音は人の声や、車の走行音など、身近なところにあふれてますね。
こういう音は必ずいくつかの周波数が混ざり合ってできています。
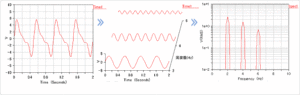
出展元:エー・アンド・ディー/FFTアナライザ入門
この図を例にとって説明します。
左のグラフはいくつかの周波数が混ざった音の波形だと思って下さい。中央の波はそれを分解したものです。
つまり左のグラフのような波形は、実は中央のグラフのように様々な周波数の波が混ざってできたものということです。
右のグラフをそれをフーリエ変換したものです。2Hz・4Hz・6Hzにピークが立っていて、この波形は3つの周波数から成り立っていることがわかります。
例えばギアから発生する音はギアのかみ合いの周波数を計算すれば、推測できます。6Hzがそれだとしましょう。(実際は歯数×回転数(rps)なので、もっと高いです…突っ込まないで笑)
ギアを回すモータの音も出るかもしれません。これを4Hzだとします。
2Hzは不明もしくはノイズだとします。
例えば、ギアが壊れて空回りしたらどうでしょう。
モータの音の周波数4Hzは消えません。でもギアのかみ合い周波数の6Hzはなくなりますよね?
逆に言うと、ギア設計からの噛み合い周波数を把握して、周波数分析を行えば、ギアが壊れているかどうかがわかる。つまり診断ができるということになります。
AIエンジニア・データサイエンティストへの道
私の場合、プログラミングの基礎はほぼ独学で学んでます。勉強法に興味のある方は読んで下さい!!

ですが…AIエンジニアやデータサイエンスの分野は独学で学ぶのは少し難しいと思います。なぜなら、プログラミングと違い、答えがないものを追うことがほとんどだからです。
勉強法を知るためにAIエンジニアになるためのロードマップを作りました。

データサイエンティストを目指す方にはこちらをお勧めしてます。

そもそも少ないデータサイエンティスト専門の講座。その中でも社会人を対象にしている講座は少ないです。このデータミックスさんでは
1. データサイエンティストとしての経験豊富な講師が実務視点でレクチャー
2. 少人数制で受講生一人一人の強みや弱みを把握したうえでの指導
3. 多くのケーススタディなどを取り扱い実践的なスタイルで実務に活きる講義内容
4. 様々な業界・職種の受講生と授業だけでなく、勉強会やイベントで交流ができる
5. 卒業後も継続したフォローアップ体制。OG・OBネットワーク。
6. 転職希望者への転職支援。
という方針でカリキュラムを実施しており、実際のケーススタディを基に講義を行うため、答えがあることを学べるのが魅力です。詳しい内容は無料説明会で公開しているようです。また、アフターケアもしっかりされており、本気で転職を目指す方にももお勧めできます。
まとめ FFT解析のポイント
- FFTは『Fast Fourier Transform』の略語。日本語にすると『高速フーリエ変換』フーリエ変換を実装するために演算を軽くしている。
- フーリエ変換を行うことで周波数領域でデータを分析できる。
- 周波数領域で分析を行うことにより、音や振動の特徴が把握でき、診断や特徴把握に繋がる。
次回は実際に音のデータをフーリエ変換する場合にフォーカスした記事を書きます。フーリエ変換をPythonで実施する方法の記事も書く予定です。そこまで読めば、あなたもフーリエ変換ができちゃいます!
座右の銘は『明日は明日の風が吹く』
虎ぱぱでした♪













 第1位 【.Pro】
第1位 【.Pro】 第2位 【TECHACADEMY】
第2位 【TECHACADEMY】
 第3位 【Aidemy】
第3位 【Aidemy】